オセロゲーム開発 ～アルファベータ法（alpha-beta search）～

このサイトでは、C言語でのオセロ（リバーシ）のプログラム開発方法を解りやすく説明しています。初級者、初心者でも作れるオセロ実装のコツが満載です。

αβ法はMINIMAX法を改良した素晴らしい探索アルゴリズムです。改良次第でより高速なプログラムを生み出すことも可能です。

最初に「オセロ（リバーシ）の作り方 ～Minimax 探索法～」を読むことをオススメします。

minimax法ゲーム木探索のおさらい

最善手を見つけるとき、相手が最善を打ったと仮定したときの、自分の最善手を検索する必要があります。これは最善手を見つけるときの基本であり、min-max法と言われます。

すなわち自分は評価関数が最大になる手を探し、相手は負に最大になる手を探すというわけです。

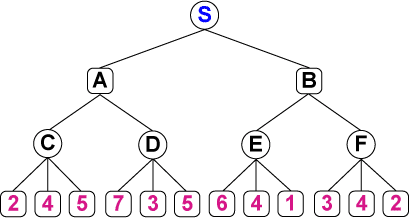
図1　minimax法 実行例

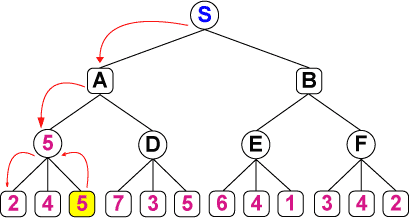
図2　minimax法 実行例

αβ（アルファベータ）法ゲーム木探索

すべての手を検索すると、莫大な時間がかかってしまいます。そこで、考え出された方法が、a-b法と呼ばれるものがあります。

a-b法はゼロ和ゲームをプログラミングする上で非常に基本的かつ重要で、その適用範囲は広いです。

図で説明します。

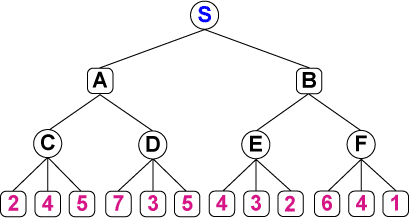
図3　アルファベータ法 を適用する評価木

最小値を求めるAでは「5」なので、Dは「7」が見つかった時点で残りの「3」「5」の探索は行いません。

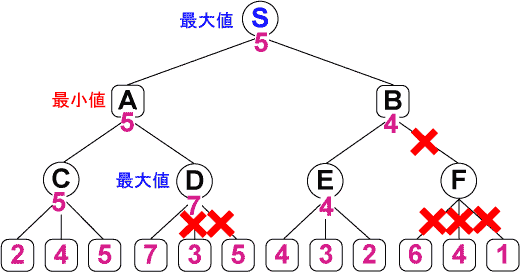
図4　アルファベータ法 実行例

また、最大値を求めるSでは「5」なので、Bは「4」が見つかった時点で「3」「2」「6」「4」「1」の探索は行いません。

なぜなら、Eで最大値が「4」の場合、「B=4」以下となります。このため「S=5」以上の値がBの枝には存在しないことが分かるためです。

まとめると、Aでは「最小値5より大きな値が見つかった時点」、Sでは「最大値5より小さな値が見つかった時点」で枝の探索を打ち切ります。

αβ（アルファベータ）法シミュレーション

より具体的な動作が分かるようにシミュレーションを用意しました。

サンプルソースコード

/******** αβ法による評価値の検出関数 *************/

int alphabeta(局面 node, 縦 row, 横 col, 手順 turn, 先読みの深さ depth, α, β)
{

  copy(局面 node, コピー局面 node);  /* コピーを行う */

  コピー row = 縦 row;
  コピー col = 横 col;

  /* 盤面の状態を送る(パスや終局等の判定を行う) */
  state = board_state(コピー局面 node, コピー row, コピー col, turn);

  if(state == END){ /* 終局の場合 */

    return(終局評価関数(コピー局面 node, turn));

  }else if(state == PASS){ /* パスの場合 */
     
    turn = turn*(-1);

  }else if(depth <= 0){ /* 最下ノード時処理 */

    return(局面の評価関数(コピー局面 node);

  }

  /* 現在の局面から1手進めた状態をa[1],a[2],a[3]とする */
  expand_node(コピー局面 node, 配列 row, 配列 col, turn, 打てる個所の数 child_count); 

  select = 0;   /* 初期設定 */
  
  /* α < β && i < child_countの時は繰り返す */
  
  for(i = 0; (α < β) && (i < child_count); ++i){
    
    inc_row = 配列 row[i];
    inc_col = 配列 col[i];
    
    val = alphabeta(コピー局面 node, inc_row, inc_col, turn*(-1), depth-1, α, β);
    
    if(turn == 先手 && val > α){
      α = val;  /* αカット */
      select = i;

    }else if(turn == 後手 && val < β){
      β = val;   /* βカット */
      select = i;
    }
  }

  縦 row = 配列 row[select];
  横 col = 配列 col[select];

  if(turn == 先手) return(α);
  else             return(β);
}

次に打った手を送る必要が無いのであれば、プログラムの下の方は簡略化され、綺麗な形にまとまります。

Negamax探索法

Negamax探索法は、基本的な考え方はαβ探索法と同じです。

違うのは、相手はこちらの利益を最小にするように打つのではなく、自分自身の利益を最大にするように打つというところです。これはMinimax探索法と同じになります。

Negamax探索法では、自分も相手も常に最大値を選ぶようになるので、プログラムが簡潔になるという利点があります。

int NegaMax(int a,int b){

  /* 葉の場合、評価値を返す */
  if(leaf()) return eval();
  else{
    int t,i;
    for(i=0;i<n && a<b;i++){
      t=-child[i]->NegaMax(-b,-a);
      if(a<t)     a=t;
    }
    return a;
  }
}

最優先探索

αβ探索においては、その局面での良い手を先に探索することが重要となります。

良い手を先に検索すれば、α-βのカット量が増しより速く効率の良い探索となる為です。

このために、いくつかの手法が使用できます。

• １）まず第一に、それぞれの手に対し「キラー応手」を保存しておく方法があります。例えば、相手がｇ２にＸ打ちしてきたときには、最初にｈ１を調べ、隅が取れないか、取るべきか考慮する方法です。

• ２）別の有用な手法として、浅い探索をしてみるというのもあります。例えば深さ１２の探索をする前に、深さ２の探索で最善と思われる手を探します。この時、深さ２の探索で掛かる時間は０秒に近いため、効率良く深い手を探索出来ます。

考慮した結果、初段程度のプログラムを作成するなら、「開放度」によるノードの並び替えが、最も効率的でした。

オススメ書籍

オセロに強くなりたい人は下記を読むことをお勧めします。

オセロ（将棋等）のプログラムを開発したい人・ゲームプログラマーになりたい人は下記は持っていて損はないでしょう。

ページの先頭へ移動